Mastering The Perimeter Formula: Your Essential Guide

Have you ever wondered how much fencing you’d need for a garden, or the length of trim required for a new picture frame? These everyday questions, and countless others, boil down to a fundamental concept in geometry: perimeter. Understanding the perimeter formula isn't just for math class; it's a practical skill that empowers you to solve real-world problems, from home improvement projects to urban planning. It's about measuring the boundary, the outer edge, the complete path around a shape. Whether you're a student grappling with geometric concepts or an adult looking to brush up on essential math skills, this comprehensive guide will demystify the perimeter formula, making it accessible and easy to apply.

In this article, we will embark on a journey to explore the fascinating world of perimeter. We’ll delve into its core definition, uncover the specific formulas for various shapes, and equip you with the knowledge to calculate the perimeter of anything from a simple square to a complex irregular polygon. We'll also touch upon practical applications, helpful tools, and common pitfalls to avoid. By the end, you'll not only understand the perimeter formula but also feel confident in applying it to any situation that comes your way.

Table of Contents

• What Exactly is Perimeter?
• The Fundamental Perimeter Formula for Polygons
• Unraveling Perimeter Formulas for Common Shapes
  • Squares and Rectangles
  • Triangles and Parallelograms
• The Special Case: Circumference of a Circle
• Navigating Regular vs. Irregular Shapes
• Practical Applications of the Perimeter Formula
• Tools and Tips for Mastering Perimeter Calculations
  • Leveraging Online Tools
  • Avoiding Common Mistakes
• Deep Dive: Derivations and Understanding the 'Why'

What Exactly is Perimeter?

At its core, the concept of perimeter is wonderfully straightforward. Imagine you're walking around the edges of a park. The total distance you cover as you complete one full loop around its boundary is the perimeter of that park. More formally, **Perimeter is the total length of the boundary of any closed shape, measured in units of length.** It's a fundamental concept in geometry, often taught alongside area, and together, these formulas are the backbone of mensuration – the branch of mathematics dealing with the measurement of geometric figures. Think of it this way: if you were to "unroll" the boundary of any shape into a straight line, the length of that line would be its perimeter. **Also, it is defined as the sum of the length of all the sides of the object.** This simple definition applies universally, whether you're dealing with a simple square or a complex, multi-sided figure. The perimeter tells you how much material you'd need to go around something, be it a fence, a ribbon, or a decorative border. **The algebraic sum of the length of each side is the perimeter of that.** This foundational understanding is crucial before we dive into the specific perimeter formula for various shapes. It sets the stage for grasping why different shapes have different formulas, yet all stem from the same basic principle of summing up boundary lengths.

The Fundamental Perimeter Formula for Polygons

While different shapes have specific formulas, there's a universal principle that applies to all polygons: the perimeter is simply the sum of the lengths of all its sides. This is the most basic and intuitive **perimeter formula**. For any polygon, regardless of how many sides it has or how irregular its shape, you can always find its perimeter by adding up the lengths of each individual side. **Formula for perimeter the perimeter of various shapes can easily be found using the formula, perimeter of polygon = sum of all sides so, if the sides of any polygon are given then its perimeter can be calculated by simply adding those lengths.** Consider a regular pentagon, a five-sided shape where all sides are equal. If each side measures 3 units, then its perimeter would be calculated as **3 + 3 + 3 + 3 + 3 = 5×3 = 15** units. This simple multiplication works for regular polygons because of their equal sides. However, for an irregular polygon, where sides might have different lengths, you would simply add each unique length. For instance, if a quadrilateral has sides measuring 4, 5, 6, and 7 units, its perimeter would be 4 + 5 + 6 + 7 = 22 units. This highlights the flexibility and power of this fundamental rule: **The perimeter of any polygon is the sum of the lengths of all the sides.** This principle is the bedrock upon which all other polygon perimeter formulas are built, providing a consistent method for calculating the boundary length of any straight-edged figure.

Unraveling Perimeter Formulas for Common Shapes

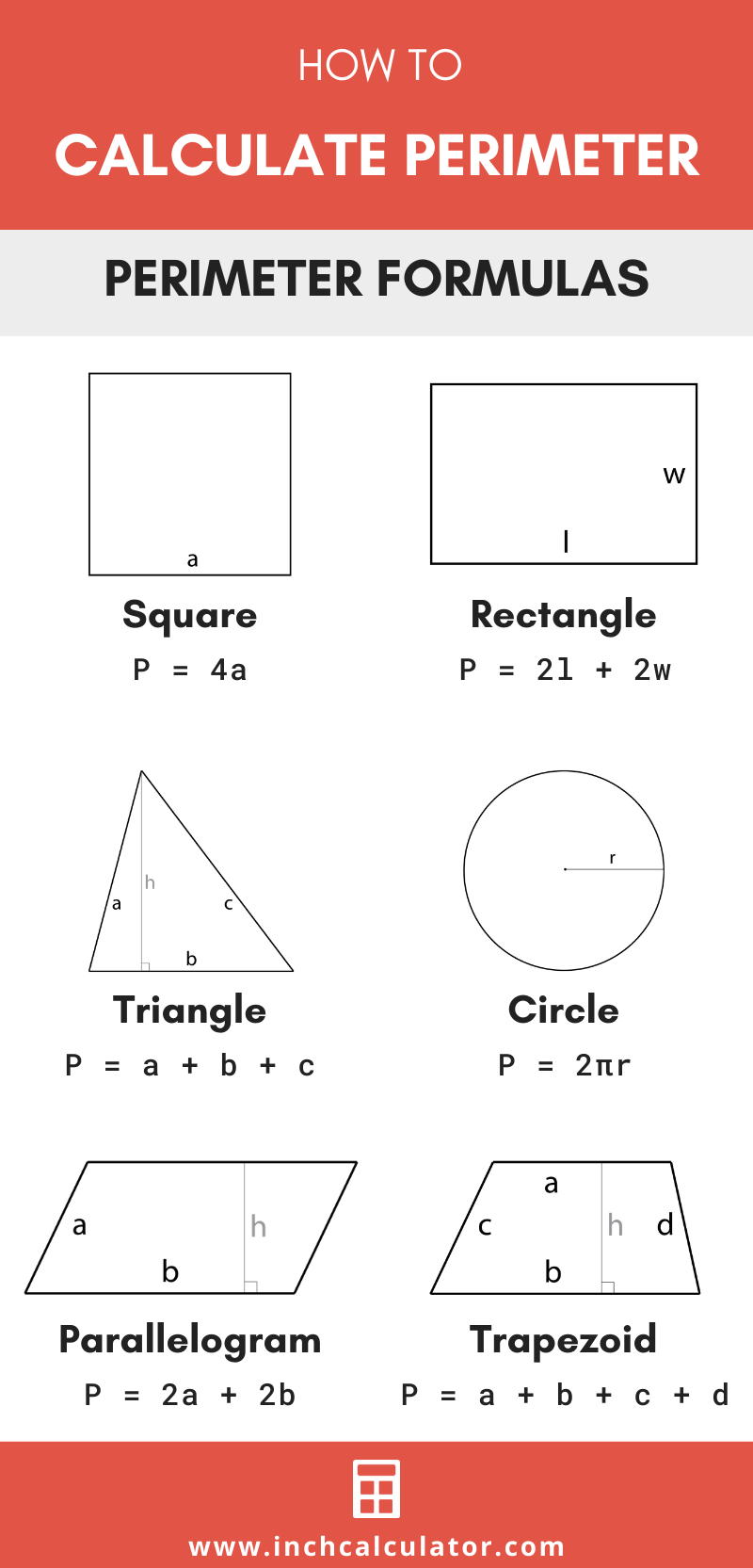
As we progress from the general concept to specific applications, it's incredibly useful to **learn the perimeter formulas for squares, rectangles, triangles, circles, ellipses, and more with examples and explanations.** While the "sum of all sides" rule is universal for polygons, specific shapes often have simplified formulas that make calculations quicker and more efficient. These tailored formulas arise from the unique properties of each geometric figure, such as equal sides or parallel sides. Mastering these specific formulas is a key step in developing your mathematical fluency and efficiency.

Squares and Rectangles

Squares and rectangles are among the most common shapes encountered in daily life, and their perimeter formulas are straightforward.

• Square: A square has four equal sides. If we denote the length of one side as 's', then the perimeter (P) of a square is simply the sum of its four equal sides:
  P = s + s + s + s = 4s
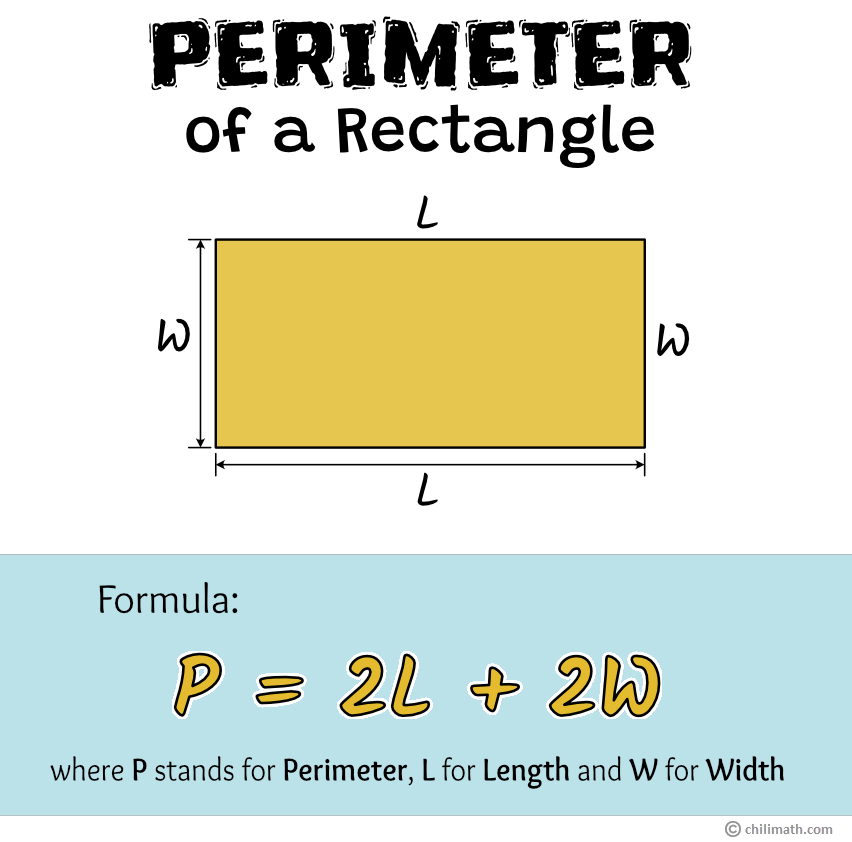
  For example, if a square has a side length of 5 cm, its perimeter is 4 * 5 = 20 cm.
• Rectangle: A rectangle has four sides, but opposite sides are equal in length. If we denote the length as 'l' and the width (or breadth) as 'w', then the perimeter (P) of a rectangle is the sum of its two lengths and two widths:
  P = l + w + l + w = 2l + 2w = 2(l + w)
  As an illustration, if a rectangle has a length of 7 units and a width of 3 units, **The perimeter of this rectangle is 7+3+7+3 = 20** units. This demonstrates the application of the formula in a clear, practical way.

These formulas are incredibly useful for practical tasks. **If we need to calculate the length of a circular or rectangular field, then with the help of the perimeter formula we can easily find it, given the dimensions.** This highlights the real-world utility of understanding these basic geometric calculations.

Triangles and Parallelograms

Moving beyond quadrilaterals, triangles and parallelograms also have distinct perimeter formulas based on their side properties.

• Triangle: A triangle is a three-sided polygon. Its perimeter is simply the sum of the lengths of its three sides. If the sides are 'a', 'b', and 'c', the perimeter (P) is:
  P = a + b + c
  For instance, if a triangle has sides of 3 cm, 4 cm, and 5 cm, its perimeter is 3 + 4 + 5 = 12 cm. For triangles where side lengths might not be directly given but coordinates are, **The perimeter of the triangle is ef + fg + eg, the lengths of which can be found using the distance formula** between the vertices.
• Parallelogram: A parallelogram is a quadrilateral with two pairs of parallel sides. Like a rectangle, its opposite sides are equal in length. If we denote the lengths of its adjacent sides as 'a' and 'b', the perimeter (P) is:
  P = a + b + a + b = 2a + 2b = 2(a + b)
  This formula is identical to that of a rectangle, reflecting the shared property of opposite sides being equal. For example, a parallelogram with adjacent sides of 6 cm and 4 cm would have a perimeter of 2 * (6 + 4) = 20 cm.

**Learn how to calculate the perimeter of a rectangle, square, triangle, parallelogram, and circle.** This foundational knowledge is essential for tackling more complex geometric problems.

The Special Case: Circumference of a Circle

While polygons have sides that can be summed, a circle is a unique shape with a continuous, curved boundary. For a circle, its "perimeter" has a special name: **The perimeter of a circle is called the circumference.** This distinction highlights the unique nature of circular measurement. Instead of summing straight sides, we use a constant value related to the circle's curvature. The formula for the circumference (C) of a circle depends on its radius (r) or diameter (d):

• Using the radius (r), which is the distance from the center to any point on the circle:
  C = 2πr
• Using the diameter (d), which is the distance across the circle passing through its center (d = 2r):
  C = πd

Here, 'π' (pi) is a mathematical constant approximately equal to 3.14159. It represents the ratio of a circle's circumference to its diameter, a constant value for all circles. For example, a circle with a radius of 7 units would have a circumference of 2 * π * 7 = 14π units, or approximately 43.98 units. Beyond circles, the concept of a curved boundary also extends to ellipses. While the exact perimeter formula for an ellipse is more complex and often involves advanced mathematics (elliptic integrals), approximations are commonly used. Understanding the circumference of a circle is a vital component of grasping the full spectrum of the **perimeter formula** and its applications across different geometric forms.

Navigating Regular vs. Irregular Shapes

When it comes to calculating perimeter, shapes are broadly categorized into regular and irregular. Understanding the distinction is key to applying the correct approach. **Learn how to find the perimeter of regular and irregular shapes using formulas and examples.**

• Regular Shapes: These are polygons where all sides are equal in length, and all interior angles are equal. Examples include equilateral triangles, squares, regular pentagons, and regular hexagons. For regular polygons, the perimeter calculation is simplified. If a regular polygon has 'n' sides and each side has a length of 's', the perimeter (P) is:
  P = n × s
  We saw this earlier with the regular pentagon example: **The perimeter of this regular pentagon** with sides of 3 units is 5 × 3 = 15 units. This shortcut makes calculating the perimeter of regular shapes very efficient.
• Irregular Shapes: These are polygons where the sides are not all equal in length, and the angles may also vary. Most real-world shapes are irregular. For irregular shapes, you revert to the fundamental definition of perimeter: the sum of all its sides. There isn't a single, neat formula like n × s. You must measure or be given the length of each individual side and then add them all together. For instance, an irregular quadrilateral with sides of 4, 6, 5, and 8 units would have a perimeter of 4 + 6 + 5 + 8 = 23 units.

The beauty of the **perimeter formula** is its adaptability. While specific formulas offer shortcuts for regular shapes, the core principle of summing all boundary lengths remains the ultimate method for any closed shape, regular or irregular. **Learn how to find the perimeter of different shapes using formulas and examples** ensures you're prepared for any geometric challenge.

Practical Applications of the Perimeter Formula

Understanding the **perimeter formula** isn't just an academic exercise; it's a vital skill with countless real-world applications. From construction to interior design, and even in everyday problem-solving, the ability to calculate perimeter is indispensable. **Area and perimeter formulas are the fundamental formulas in mensuration that help us calculate the area and perimeter for any geometric shape in mathematics.** They provide the tools to quantify the physical world around us. Consider these practical scenarios:

• Construction and Home Improvement:
  • Fencing: Determining how much fencing material is needed to enclose a yard or garden.
  • Framing: Calculating the length of wood or metal required to frame a picture, a door, or a window.
  • Baseboards and Trim: Measuring the length of baseboards or decorative trim needed for a room.
  • Landscaping: Planning the border for a flower bed or a pathway.
• Sports and Recreation:
  • Track and Field: The perimeter of a running track defines the distance of a race.
  • Sports Fields: Marking the boundaries of a soccer field, basketball court, or tennis court.
• Design and Manufacturing:
  • Fabric and Sewing: Estimating the amount of trim, lace, or binding needed for clothing or crafts.
  • Packaging: Designing boxes or containers where the perimeter of the base or opening is a critical dimension.
• Urban Planning and Mapping:
  • Property Lines: Defining the boundaries of land plots.
  • Route Planning: Calculating the length of a walking or driving route.

As you can see, **Perimeter the perimeter is an important concept in geometry** that extends far beyond the classroom. It provides a tangible way to measure and understand the boundaries of objects and spaces, making it an invaluable tool for professionals and individuals alike. **Learn how to calculate the perimeter of various geometric shapes, such as squares, rectangles, triangles, polygons, and circles**, equips you with a skill that will serve you well in numerous practical situations.

Tools and Tips for Mastering Perimeter Calculations

Calculating perimeter, especially for complex shapes or when precision is paramount, can sometimes benefit from modern tools and careful practices. While a ruler is your primary tool for direct measurement, digital resources and smart habits can significantly enhance your accuracy and efficiency.

Leveraging Online Tools

In today's digital age, you don't always need to manually crunch numbers. Several online resources can assist you. **Find the perimeter of any geometric shape using this online tool** can be a great starting point for quick checks or for shapes with complex coordinates. These tools are designed for user-friendliness and accuracy. For instance, **Use this online tool to calculate the perimeter of common geometrical shapes like square, rectangle, triangle, circle, and more.** These calculators often require you to input the relevant dimensions (side lengths, radius, etc.) and instantly provide the perimeter. Furthermore, **An easy to use, free perimeter calculator you can use to calculate the perimeter of shapes like square, rectangle, triangle, circle, parallelogram, trapezoid, ellipse, octagon, and sector of a circle** can be incredibly helpful for students, DIY enthusiasts, or anyone needing a quick, reliable calculation without the risk of manual error. Many of these tools also **learn the formulas, explanations, and graphs for each calculation with examples and tips**, turning them into interactive learning resources.

Avoiding Common Mistakes

Even with simple formulas, errors can creep in. Here are some common pitfalls and how to avoid them:

• Unit Conversion: One of the most frequent mistakes is mixing units. If some measurements are in meters and others in centimeters, convert them all to a single unit before calculating. **Find out how to convert units and avoid common mistakes in math problems.** Always ensure consistency.
• Missing Sides: For irregular polygons, ensure you've accounted for every single side. It's easy to overlook one side in a complex drawing. Double-check your diagram against your list of side lengths.
• Confusing Perimeter with Area: These are two distinct concepts. Perimeter measures the boundary, while area measures the surface inside the boundary. Ensure you're applying the correct **perimeter formula** for the task at hand.
• Incorrect Formula Application: For shapes like rectangles, remember it's 2(l+w), not just l+w. For circles, use the correct circumference formula (2πr or πd).
• Measurement Accuracy: When measuring manually, use a reliable tool like a ruler or tape measure. **Find out how to measure the perimeter using a ruler** accurately, ensuring your measurements are precise.

By being mindful of these tips and leveraging available tools, you can significantly improve the accuracy and efficiency of your perimeter calculations.

Deep Dive: Derivations and Understanding the 'Why'

While knowing the **perimeter formula** for various shapes is essential, truly understanding them involves grasping *why* these formulas work. This often means looking at their derivation – how they are logically constructed from fundamental principles. **Understand the perimeter formula with derivation, examples, faqs** is a crucial step in moving from rote memorization to genuine comprehension. Let's consider the derivation of a few common formulas:

• Rectangle (P = 2(l + w)): This formula directly stems from the definition of perimeter as the sum of all sides. A rectangle has two lengths (l) and two widths (w). So, P = l + w + l + w. By combining like terms, we get P = 2l + 2w. Factoring out the common '2' gives us P = 2(l + w). This derivation clearly shows how the formula is a simplified representation of adding the four sides.
• Square (P = 4s): A square is a special type of rectangle where length equals width (l = w = s). Substituting 's' into the rectangle formula P = 2(s + s) gives P = 2(2s) = 4s. This shows the square's formula is a specific case of the rectangle's.
• Circle (C = 2πr or C = πd): The derivation of pi (π) and the circumference formula is more complex, rooted in calculus and the concept of limits. Historically, mathematicians observed that the ratio of a circle's circumference to its diameter was always a constant, regardless of the circle's size. This constant was named pi. So, C/d = π, which rearranges to C = πd. Since the diameter is twice the radius (d = 2r), substituting this into the formula gives C = π(2r) or C = 2πr. This derivation connects the abstract constant pi to the tangible measurement of a circle's boundary.

Understanding these derivations reinforces the logic behind each **perimeter formula**. It helps you see that these aren't arbitrary rules but rather logical consequences of the shapes' properties. This deeper understanding builds confidence and makes it easier to recall and apply the formulas correctly, even for less common shapes like parallelograms, rhombuses, trapezoids, and regular polygons. **Learn how to calculate the perimeter of triangles, squares, rectangles, parallelograms, rhombuses, trapezoids, circles and regular polygons. See the formulas, examples and diagrams for each shape.** By understanding the 'why,' you're not just memorizing; you're truly learning.

Conclusion

We've journeyed through the fascinating world of perimeter, from its fundamental definition as the total length of a boundary to the specific formulas that simplify calculations for various geometric shapes. We've seen that the core principle for polygons is always the sum of all sides, beautifully encapsulated by the general **perimeter formula**: perimeter of polygon = sum of all sides. For circles, this boundary length takes on a special name – circumference – and is calculated using the constant pi. The ability to calculate perimeter is more than just a mathematical exercise; it's a practical skill with immense utility in everyday life, from planning home projects to understanding architectural designs. Whether you're using a simple ruler or leveraging an online calculator, mastering the **perimeter formula** empowers you to accurately measure and quantify the world around you. Now that you've explored the ins and outs of perimeter, why not put your newfound knowledge to the test? Try calculating the perimeter of objects around your home, or use an online tool to check your answers. We encourage you to share your thoughts, questions, or any interesting applications of perimeter you've discovered in the comments below. And if you found this guide helpful, consider sharing it with friends or family who might also benefit from understanding this essential mathematical concept. Explore other articles on our site to continue your journey into the captivating world of mathematics!